, to all possible pairs of intermediate destinations q
and r is given by the formula
Heinz Spiess
EMME/2 Support Center, Haldenstrasse 16, CH-2558 Aegerten, Switzerland
March 1993
Revised April 1995
Revised November 1996
In this note we look at a logit type choice model for simultaneously choosing the N-1 intermediate destinations in an N-legged activity chain. We reformulate the model in terms of matrix products, and show how the demand matrices corresponding to the individual legs of the activity chain can be computed efficiently. An extension of the model for simultaneous destination and mode choice is also discussed, as well as the special case of mixed mode trip chains.
A PDF version of this document is also available.
Traditional trip distribution models models typically consider only trips to a single destination for the purpose of carrying out a single activity (such as work, shopping, leisure, ...). While this simple model of a trip represents quite well a large fraction of the trips that are subject of travel demand models, many ``real life'' trips combine more than one activity carried out at more than one destination (such as stopping at the shopping center on the way back from work). For this purpose, trip distribution models based on activity chains have been developed and used extensively in the past (see e.g. Adler and Ben-Akiva 1979, Clarke et al. 1981, Pas 1984, ...). Most of these models are stated in the form of a multinomial logit model, in which each possible trip chain constitutes a possible choice.
In the practical implementation of these models, however, the underlying simultaneous choice model is often approximated by using a sequential choice model , in which the decision on the n-th intermediate destinations is dependent only on the n-1 previous destinations in the activity chain, but not on the destinations still ahead. It is well known (Domencich and McFadden, 1975) that under certain conditions, simultaneous logit choice models can be broken into a series of sequential sub-models. This is basically the case when the individual decisions are mutually independent. In the case of a trip chain, however, this mutual independence is clearly not given, since it is broken by the fact that the trip chain always has to end at the very same point it started out. Also, as Takahashi (1988) points out, there is empirical evidence that the choice of a destination depends substantially on the utility of possible later destinations on the same trip chain.
Nevertheless, in most practical implementations of trip chaining models, the decision making process is in some form sequentialized, in spite of the fact that this introduces approximations to the model computations.
In the following sections of this note, we will show how trip distribution models based on trip chaining can be implemented keeping their full simultaneous nature, without need for any sequentialization of the decision taking process.
Let us first look at the special case of an three-legged activity chain. Starting at the origin p, the first leg of the trip goes to the intermediate destination q, where the first activity takes place; then continues to the intermediate destination r where the second activity is carried out, and finally returns back to the origin p.
Note that we shall assume that all zone indices (such as p, q and r) always imply a zone of the same underlying zone subdivision.
The logit model for distributing the total production of trip chains starting
at origin p, , to all possible pairs of intermediate destinations q
and r is given by the formula
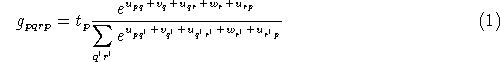
where 
, 
and 
represent the utilities (or rather the
negatively weighted disutilities) associated with travelling on the three legs
of the trip chain (pq), (qr) and (rp). The utility associated with
carrying out the first activity at destination q is 
and the
utility of carrying out the second activity at destination r is 
.
, finally, represents the total production of trips at origin p.
Note that, without loss of generality, we can assume the utilities u, v
and w to represent the weighted sum of all pertinent variables.
Since the exponential of the sum of the various utilities can be reformulated
as the product of the exponentials of each utility, it is useful to restate
in terms of the transformed variables 
, 
and 
, which yields
The above formulation shows well that the the logit model with its additive character of the utility is indeed a multiplicative model in which the activities to chose from are represented by factors. Thus, it is to be noted that the discussion which follows is not limited to logit models, but is equally applicable to any model of the form (2).
The denominator of (2), which represents to total weight of all
possible choices of intermediate destinations for trip chains starting
at p, will be denoted by 
While the basic result of model (2) are the number of trips
( 
) for each possible chain pqrp, what for practical purposes
is needed are the three demand matrices that correspond to the travel on
each of the three legs of the trip chain, i.e.
It is interesting to note that the above relationships can also be formulated
using matrix notation. For this purpose, we introduce the following matrices:
C is the conductivity matrix 
;
A is the diagonal matrix containing attractivities 
;
B is the diagonal matrix containing attractivities 
;
and finally T is the diagonal matrix containing total productions .
Using matrix notation
corresponds to the matrix of the total weights for all 3-leg trip chains
starting at zone p and ending at zone q. The diagonal elements of
S, therefore, correspond exactly to defined in (3)
For convenience, we introduce the diagonal matrix containing the normalized trip generation rates as
For the demand matrices that correspond to the 3 legs of the trip chain rewriting of equations (4) - (6) in matrix notation yields
where the operator 
indicates element by element multiplication
of the corresponding matrix operands, i.e. 
.
This model for a 3-legged activity chain has been implemented
in a macro for the EMME/2 transportation planning system. The macro is
called
TCHAIN3
and is available on the
Web site of the EMME/2 Support Center.
Having dealt explicitly with the special case of 3-leg trip chains, it is now relatively straight forward to extend the results to the general case of trip chains having N legs and N-1 intermediate destinations.
We shall denote 
, 
, ..., 
the diagonal matrices containing
the attractivities of the zones for activities of the type n, 
.
The total weights of all possible N-leg trip chains between any pair of zones is given by
Again, it is convenient to introduce the diagonal matrix containing the
normalized trip generation rates, but for the sake the symmetry in the
notation, we shall call it 
Assuming that all indices of the matrix A are to be taken modulo N
(i.e. 
),
the demand matrix corresponding the the n-th trip leg, 
can be written as
It is easily possible to generalize this type of distribution model to
simultaneously include mode and destination choice. For the purpose,
we assume that M travel modes are available to the traveller. For each mode
m, a conductivity matrix 
is constructed from the mode specific
travel cost matrix. In addition, each for each origin p and each mode m,
the variable 
represents the attractivity bias of mode m to the
travellers from origin p (i.e. the combined effect of the mode dependent
socio-economic variables at origin p). Let 
denote the diagonal
matrices containing these bias variables for mode m.
We shall denote 
the diagonal matrices containing
the attractivities of the zones for activities of the type n and travel
by mode n. Note that these attractivities can vary with the mode used
(e.g. parking availability of cost), but they don't have to necessarily.
The total weights of all possible N-leg trip chains of all modes between any pair of zones is given by
Again, it is convenient to introduce the diagonal matrices containing the normalized trip generation rates for mode m as
Using again the modulo N convention for the first subscript of A,
the demand matrix corresponding the the n-th trip leg,
can be expressed as
The type of analysis presented in the previous sections can of course also be applied to trip chains in which more the one mode is used within the same trip chain. A typical example for this category of problems is the choice of the parking site for park+ride travellers, is is briefly outlined in this section.
We assume the following logit model for choosing between parking sites:
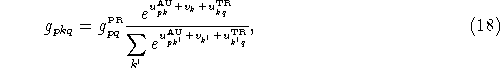
where 
corresponds to the number of trips between p and q
choosing parking site k according to the mode specific utilities
(auto mode) and 
(transit mode)
and the attractivity variable of parking at zone k, 
.
Using the transformed variables
,
and
, we obtain
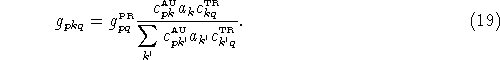
In matrix notation, the denominator can be written as
and the matrix 
is defined as
where the operator 
is used to indicate element-by-element division.
The intermediate auto and transit demand matrices resulting from the above
model can now be written in matrix notation as
The average auto and transit impedances for the park+ride
trips from p to q, 
and 
,
can be computed as
whereas the average parking cost paid by park+ride trip from p to q is
In matrix notation, the park+ride impedance and cost matrices can be written as
Note that the above formulae are not limited to compute the impedances and parking costs of the park+ride trip, but they can also be applied to any other auto or transit attribute, such as distance or fare, by simply substituting the matrix U by the corresponding attribute matrix.
The computations of the first and secord leg intermediate matrices
for mixed mode trips according to (22) and (23) have
been implemented in a macro for the EMME/2 transportation planning system.
The macro is called
MIMOLEG
and is available on the
Web site of the EMME/2 Support Center.
Note that the model presented in this note do not consider any capacities limitations at parking lots. For a detailed discussion of modeling mixed mode trips with explicit capacities at intermediate destinations see Spiess (1996).
We have shown that logit type distribution models that are based on activity chains can computed directly without any need to approximate the behavioral assumptions through the introduction of a sequential decision model. Thus the traveller decides for a trip chain in its entity, i.e. all intermediate destinations (as well as the mode, in the case of a combined model) are chosen simultaneously.
We showed that these models can be reformulated as simple matrix expressions, involving only simple operations such as algebraic matrix multiplications and element-by-element matrix multiplications. This also means that they can be efficiently implemented in any transportation planning software packages which includes matrix calculation facilities which include these two types of operations. The EMME/2 transportation planning system (Spiess 1984, INRO 1992) includes very flexible matrix manipulation tools. These have been used to implement activity chain based distribution models by directly applying the formulae developed in the preceding section. Macros have been written to automate the computations. This shows that direct implementation of activity chain based trip distribution models are not just theoretically possible, but also practically feasible, even for large scale applications.
